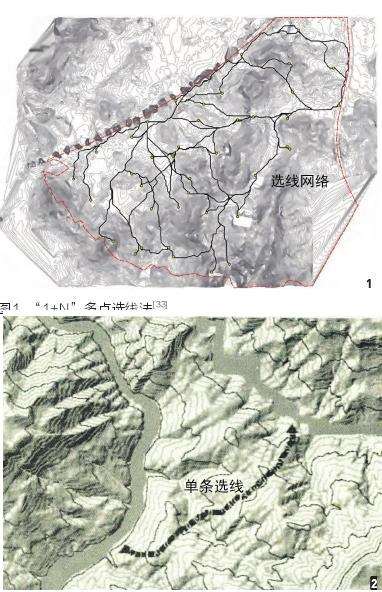
根据袁旸洋等研究[33]，本实验中涉及的道路可定义为“风景环境道路”，关于风景环境道路选线研究主要集中在GIS和Rhino+Grasshopper[34]的参数化选线。GIS选线是基于逻辑运算的自动化过程，其受限于地形、地质、水文、土地利用、交通等多因子影响。袁旸洋在研究区域内设置多个道路起点、终点、控制点，并通过“1+N”多点多次选线方法，完成风景区内多条道路选线，最终形成覆盖全区域的选线路网，通过路网构建道路模型实现区域内道路规划，如图1所示。同时，在汤国安[35]路径选线实验中，通过设定目标点位置(源点、终点)，运算形成一条路径选线，如图2所示。

这2种方法是GIS风景环境道路选线设计代表性的方法，都是基于影响因子权重叠加的选线过程，核心差异并不完全体现在路网模型和单条道路选线模型。本实验中，汤国安单条选线法通过多次重复与路径叠加后可以实现袁旸洋路网模型，相比2种选线途径其底层逻辑相同，汤国安选线方法广泛地应用在地理相关研究领域，袁旸洋将类似的选线方法进行了创新研究应用，通过“1+N”多点多次选线方法，一次性实现多点选线的设计过程。

 

本实验应用汤国安选线方法进行选线实验。实验区域内重要的景观节点位置、景区出入口位置等都可以成为选线考量的重要节点，实验区域内设置了多个选线节点，其位置有如下2种设计。

 

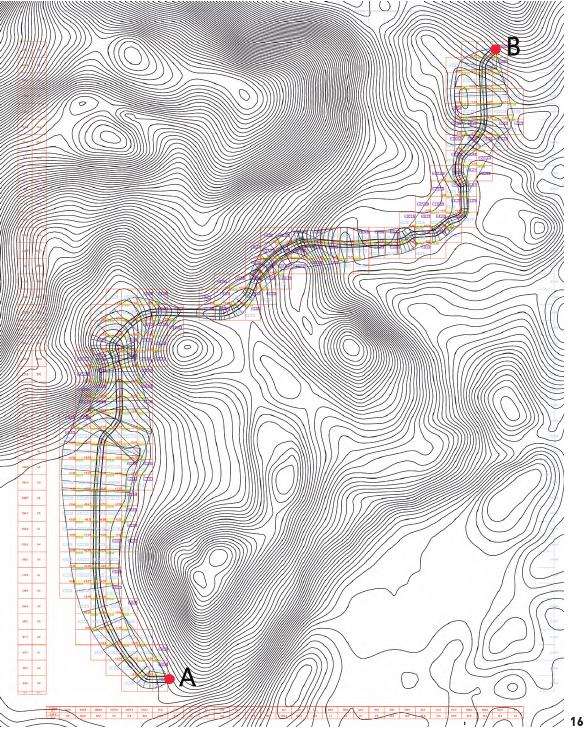
1)在原始地形上任选3对路线始末位置点分别为AB、CD、EF，如图3所示。AB、CD、EF连线所过之处均有代表性的山地起伏地形，如图4红绿蓝阴影区域所示。

 

 

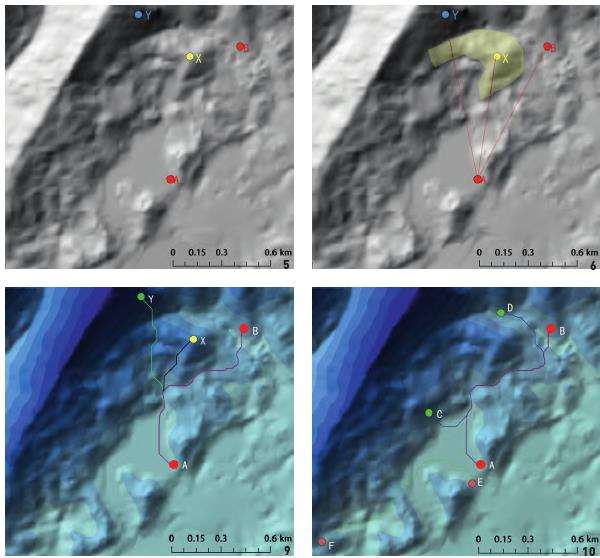
2)以A点为起始点，任选3个终点位置X、Y、B，如图5所示，进行连接后得到图6，其终点位置代表了山地地形中平缓位置(B点)、局部山顶位置(X点)、山坡位置(Y点)。依据汤国安最佳路径计算方法，通过GIS计算得到了AB、CD、EF、AX、AY共5条选线。图7、8蓝色底图为栅格计算图，蓝色深浅代表了基于高程和坡度因子在地形图上的权重反映。颜色变深说明坡度和高程值同向变大，颜色变浅意味着两者同向变小或反向变化，其中，反向变化位置集中在山顶区域，如图7中P位置所示浅色区域，其坡度值与高程值呈现反向变化。

通过图7中3条选线发现，选线AB、CD、EF均计算选择了坡度和高程同向减小的浅色区域，在地形起伏变化的空间范围内，通过栅格计算合理规避了坡度、高程因子对道路选线的不利影响，计算规划出基于高程、坡度因子影响下的道路选线结果。



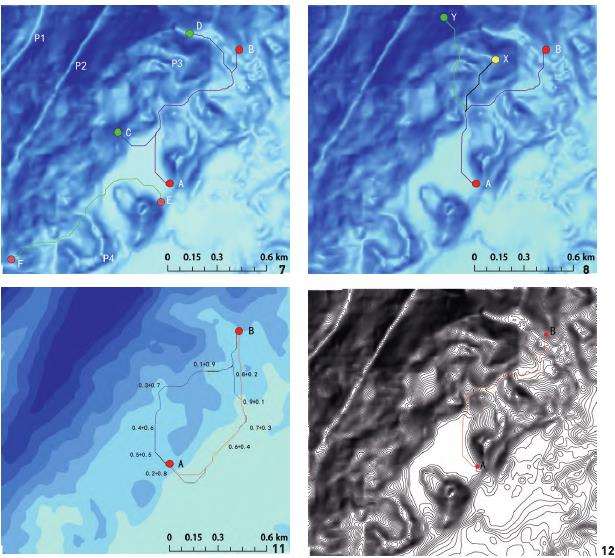
图9所示为以A为起始位置，以B、X、Y为终点的道路选线结果，通过栅格计算3条选线均规避了高程、坡度因子对选线的不利影响，所过之处均为颜色较浅范围。此外，汤国安选线方法是单条路线的选线结果，通过多次叠加后仍然可以形成路网结构，如图10所示。

 

 

影响因子权重值是选线设计的关键数据，一条道路选线受到多因子共同制约，如坡度、高程、起伏度、植被、土地利用等，合理选择因子权重直接影响选线结果。常见选线因子权重的方法集中在经验法、层次分析法、调查统计法、专家打分法等。其中，层次分析法(AnalyticHierarchyProcess，AHP)是美国运筹学专家萨蒂于20世纪70年代提出的一种层次权重决策分析方法，这种方法基于专家意见与分析者判断权重因子，其底层逻辑仍然基于人为判断。以上实验方法说明，虽然GIS选线结果是基于数学运算的自动过程，但在因子权重设定环节上，主观因素影响了GIS选线的核心过程。

 

汤国安GIS选线实验对因子权重采用经验法处理，本实验在此基础上跳出权重经验数值的束缚，探究0~1范围内尽可能多的权重值，并对不同权重下产生的选线进行分析对比，讨论选线与因子权重的关系。本实验中5条选线路径都是基于高程0.5+坡度0.5的权重进行的栅格计算，这种权重值分配只代表了权重方案中的一种经验可能。



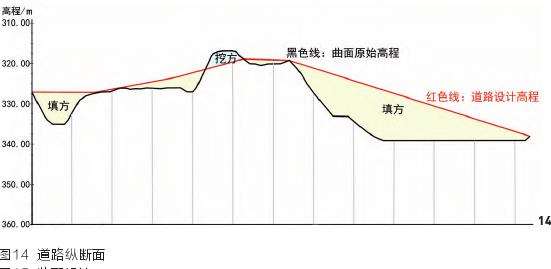
以选线AB为对象进行9组权重数据比较，如表1所示，这9组数据代表了AB间“高程+坡度”因子权重影响下选线分布情况，最终得到与之对应的9条栅格路径(图11)。实验发现，4条栅格路径全部集中在图11所示AB右侧，权重分别是0.6+0.4、0.7+0.3、0.8+0.2、0.9+0.1；有5条栅格路径集中在AB左侧，它们的权重分别是：0.2+0.8、0.5+0.5、0.4+0.6、0.3+0.7、0.1+0.9。

当高程权重小于等于0.5时，路径差异不明显，选线几乎全部重叠在一起。这说明，相同因子、不同权重值可以产生差异不显著的选线(权重不同但选线相似)，权重值与选线路径并不一定构成一一对应的关系。通过高程分析，A、B2点位于348m高程范围内，当高程权重大于坡度权重时，选线集中在高程介于329~348m的地段范围内；当高程权重小于坡度权重时，选线集中在348~370m地段范围内。此外，本实验方法是基于坡度、高程因子权重，也适用于多因子影响的选线设计，需要在栅格计算中将“1”值进行多因子权重分配。

 

应用AB选线数据，通过矢量化过程实现GIS-BIM数据交互，在BIM平台得到AB高程参数信息，这说明Civil3D成功拾取了基于GIS分析的参数值，BIM数据匹配了GIS分析结果，BIM与GIS在栅格、矢量维度上实现了数据的传递。

 

本实验数据只涉及线性栅格、矢量数据的交互，但这并不代表GIS-BIM数据交互的核心内涵。研究证实[36]，全方位的GIS-BIM数据交互并实现信息共享需要建立在数据标准基础之上，现阶段，IFC(工业基础类)和CityGML(城市地理标记语言)分别是BIM、GIS行业数据标准，IFC与CityGML所涉及的对象与数据类型也是多样化的，如应用场景、几何拓扑、语义表达、模型语言等。

2种数据标准既有区别又有交集，由于GIS面向地理环境分析与评价，而BIM主要解决模型设计与管理，当两者进行数据交互融合时可能产生诸多表达上的冲突。例如，一个完整的建筑BIM模型与GIS交互时，可能对建筑材质、坐标等数据产生差异化表达，这使得GIS-BIM数据交互受挫，行业研究曾尝试多种方法实现数据的全面交互融合。期间，ElMekawy提出了一种整合IFC和CityGML的语义类型[37]；Nagel通过设计格式转换工具实现IFC到CityGML转换[38]；Berlo使用CityGML中的ADE(ApplicationDomainExtension)储存IFC数据[39]。这些方法促进了GIS-BIM数据交互，但实现GIS-BIM数据的全面交互融合还需进一步研究。

本实验结果表明，虽然GIS-BIM全方位数据交互存在技术上差距，但这并不妨碍在低维度进行的数据交流，实验证实了线性(栅格、矢量)数据交互与转换，同理推断，GIS+BIM协同处理基于线的“面”数据也是可能完成数据交互与转换的，这为GIS+BIM协同的景观参数化设计带来更多的可能，如线性数据向“面”数据的拓展、基于线的“面”要素数据提取与交互等，这些技术路径的解决可以为诸如GIS场地选址、建筑规划、风景区规划等问题提供更加优质的解决方案。

 

 

 

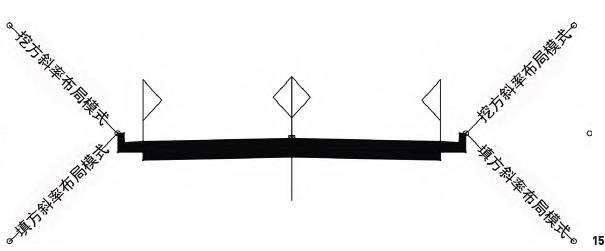
基于GIS-BIM数据交互，在BIM平台完成了道路中心线的拾取，如图12、13红色曲线所示，纵断面设计如图14所示，装配设计如图15所示，并得到了山地道路土方施工(图16)，这仅代表了部分BIM参数化设计成果，通过BIM山地模型集成了诸如放坡关系、工程填挖方量、道路长度、结构、材质、山地坡向、坡度、高程等参数信息，通过参数更新与优化实现对规划设计的精准控制。

 

道路建模是本实验的关键内容，通过BIM模型实现了基于AB选线的道路参数化设计。关于BIM道路模型设计研究，黄炎等通过BIM完成对道路沿线地形、仿真交通流等环境模拟，从而优化提高了道路设计的安全水平[40]；KarenCastaneda应用BIM模型构建了基于道路交叉口“模拟-分析-标定”的模拟框架，加深了设计者对环境地理的认识并加速了设计进程[41]；JuanF.Dols借助BIM模型创建虚拟道路场景，并将其加载到驾驶模拟器中进行模拟，提升了道路设计安全性[42]。此外，张欢欢等通过BIM模型完成对道路工程建设时间的优化设计[43]；文雅等通过降雨模拟，优化道路设施的集排水能力[44]。



以上研究表明，借助BIM平台，实现了对模型模拟与优化，提升了参数化设计的科学性与安全性。在本实验中，BIM模型实现了土方平衡计算、山地曲面、道路曲面(图17)、交通驾驶模拟(图18)、道路对象的优化设计(图19)，完成了山地模型可视化、协同、模拟等过程，并将模型信息应用于设计与反馈。

 

此外，本实验借助BIM平台完成了基于GIS选线的山地风景环境道路参数化设计，使得GIS分析数据完全参与后期的设计编辑，GIS分析数据在BIM平台得到更大拓展与延伸，并响应了“设计基于客观分析”的规划共识。